Kako pronaći područje jednodijelnog trokuta

Matematička, a posebno geometrija premaanketama školskih učenika, jednoj od najpoželjnijih lekcija, a sve zato što vas upoznaju s velikim brojem formula koje u životu 90% odraslih odraslih osoba nije pronašlo praktičnu primjenu. Ali, na trenutak, naučimo formule, rješavamo probleme, ne stvaramo jednadžbe ne zbog činjenice da nam oni mogu biti korisni u životu, već zato što razvijaju razmišljanje i logiku. Čak su i drevni grčki mudraci rekli da se ljudski um može mjeriti poznavanjem matematičkih znanosti. A kako ste se odlučili upoznati sa primjenom formula za jednodijelni trokut - mi se držimo u ruci i čitamo cijeli članak.
Prije nego počnete odgovoriti na pitanje kako pronaćipodručje jednodijelnog trokuta i idi na praktični dio članka, gdje se daju formule i izračuni, označimo sam koncept za sebe. Isosceles trokut je trokut u kojem su dvije od tri strane jednake duljine, zove se bočne strane. U slučaju redovitog trokuta, gdje su sve strane jednake, također se smatra jednako, ali obratno, kada se jednodijelni trokut smatra ispravnim - lažno.
Stranice trokuta trebaju biti označene, tako ćemo to učiniti, kao što je prikazano na donjoj slici, gdje: a-strane, b-baze i visina h.
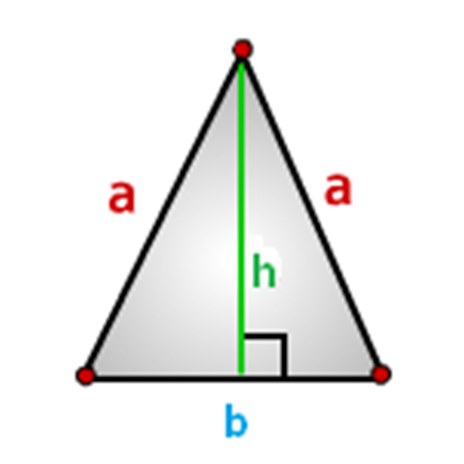
Kako izračunati područje jednodijelnog trokuta, formule.
Nakon što smo napravili notaciju visine, strane i kuta, možemo početi riješiti problem.
Za početak ćemo odrediti ono što znamo.
Ako visina i dno - onda klasična formula (* - znak množenja):
S = ½ * b * h
Zamijenimo, na primjer, brojeve gdje: h = 16, b = 18 dobivamo sljedeće:
S = ½ * 18 * 16 = 9 * 16 = 144;
Područje jednodijelnog trokuta je S = 144 cm2
Postoje i druge formule koje će nam pomoćikako znati područje podjednakog trokuta. Jedna takva formula je Heronova metoda. Nemojmo napisati složenu formulu, uzeti smo, na osnovu, skraćeni:
S = ¼ b √4 * a2-b2
Jasno je da je b temelj, i - jednake strane. Formula je pogodna u slučaju kada je visina h nepoznata.
Zamjenjujući vrijednosti, neka a = 6, b = 3 dobivamo sljedeće:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Možete izračunati područje jednako stranama trokuta i kutu između strana:
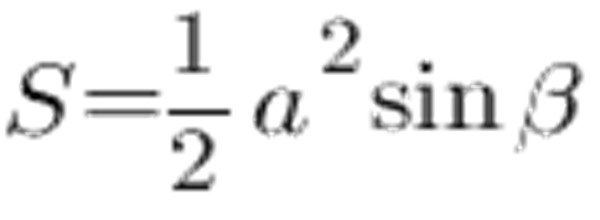
Prema sinusnom stolu, kut na 45 ° jednak je 0.7071, a strana a i neka bude 6 cm, dobijemo sljedeće:
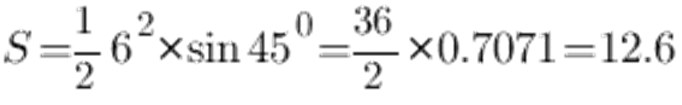
Kao rezultat toga, površina jednodijelnog trokuta je 12,6 cm2.
Postoje i načini za izračunavanje područja, uključujućiuključujući u slučaju jednodijelnog trokuta, ali su prilično složeni i ne primjenjuju se na "elementarne" izračune, kao što su one dane gore, u pojmu složene matematike. I ne vrijedi govoriti o stvarima koje čak ni učitelji s iskustvom neće razumjeti.
Dakle, možete disati uzdah olakšanja, na ovommali tok geometrije u pronalaženju područja jednodijelnog trokuta smatrat će se potpunim, a znanje stečeno kao rezultat čitanja članka naučeno je "pet".